Een enkele foton dat door een vacuüm wordt verspreid kan een roodverschuiving ondergaan in verschillende manieren. Elk van deze mechanismen produceert een Doppler-achtige roodverschuiving wat betekend dat z onafhankelijk is van de golflengte. Deze mechanismes worden omschreven als Galileo, Lorentz of algemene relativistische transformaties tussen een referentieframe en een ander referentieframe.
Overzicht roodverschuiving
| Type roodverschuiving | Transformatieframe | Meetkunde | Definitie |
|---|---|---|---|
| Doppler roodverschuiving | Galileïsche transformatie | Euclidische ruimte | 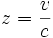 |
| Relativistische Doppler | Lorentz transformatie | Minkowski ruimte | 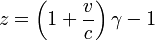 |
| Kosmologische roodverschuiving | Algemene relativistische transformatie | Friedman-Robertson-Walker meetkunde |  |
| Gravtiationele roodverschuiving | Algemene relativistische transformatie | Schwarzschild meetkunde | 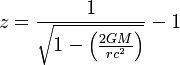 |
Het Doppler effect
Als een lichtbron zich van een waarnemer weg beweegt dan gebeurt er een roodverschuiving (z > 0), indien de bron naar de waarnemer beweegt dan gebeurt er een blauwverschuiving (z 0). Dit gebeurt bij alle elektromagnetische golven en wordt verklaard door het Doppler effect. Deze soort wordt dan ook de Doppler roodverschuiving genoemd. Indien de bron zich verplaatst van de waarnemer weg met een snelheid v dan, nu even niet rekening gehouden met relativistische effecten, wordt roodverschuiving berekend door:
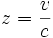
waar c staat voor de snelheid van het licht. In het klassieke Doppler effect wordt de frequentie van de bron niet aangepast maar de beweging zorgt voor een illusie van een lagere frequentie.
Relativistische Doppler effect
Een meer complete behandeling van de Doppler roodverschuiving vereist dat aanzienlijke relativistische effecten bijgestaan worden door de beweging van bronnen dicht bij de snelheid van het licht. Om het kort samen te vatten zullen objecten die ongeveer aan de snelheid van het licht bewegen afwijkingen ondergaan van de vorige formule, dit door de tijdsdilatatie van de speciale relativiteit, dit kan aangepast worden door de Lorentz factor in de klassieke Doppler formule toe te passen als volgt:
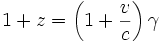
Dit fenomeen werd voor het eerst waargenomen in een experiment anno 1938 door Herbert E Ives en G.R. Stilwell, het experiment had de naam Ives-Stilwell experiment.
Aangezien de Lorentz factor enkel afhankelijk is van de magnitude van de snelheid zorgt dit ervoor dat de roodverschuiving verbonden met de relativistische correctie onafhankelijk is van de richting van de bronbeweging. In contrast met het klassieke deel van de formule is deze afhankelijk van de projectie van de beweging van de bron in het gezichtsveld welke verschillende resultaten voor verschillende richtingen uitkomt. Voor een object dat zich beweegt op een hoek θ naar de waarnemer (nul-hoek is direct weg van de waarnemer) zal de volledige formule voor het relativistische Doppler effect als volgt worden:
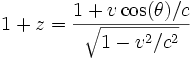
In een speciaal geval waar de bron loodrecht beweegt (θ = 90°) naar de detector wordt de relativistische roodverschuiving gekend als de transversale roodverschuiving, er wordt dan ook een roodverschuiving opgemeten, zelfs als het object niet van de waarnemer weg beweegt. Indien de bron naar de waarnemer toe beweegt, als er een transversaal component aan de beweging hangt, dan is er wat snelheid waarop de uitzetting de verwachte blauwverschuiving annuleert en op een hogere snelheid de bron een roodverschuiving ondergaat.
Uitzetting van de ruimte
In het vroege deel van de twintigste eeuw deden Slipher, Hubble en anderen de eerste metingen van roodverschuiving en blauwverschuivingen van sterrenstelsels verder dan onze melkweg. Ze interpreteerden deze eerst enkel als gevolg van het Doppler effect, maar later ontdekte Hubble een correlatie tussen de toenemende roodverschuiving en de toenemende afstand van sterrenstelsels. Theoreticussen realiseerden meteen dat deze waarnemingen verklaard konden worden door een verschillend mechanisme voor roodverschuiving te genereren. Hubbles wet van de correlatie tussen roodverschuiving en afstanden is het vereiste model in de kosmologie afgeleid van de algemene relativiteit die een metrische uitzetting van de ruimte hebben. Als resultaat worden fotonen die door de ruimte reizen uitgerokken en voor de kosmologische roodverschuiving zorgt. Dit verschilt van het Doppler effect roodverschuiving zoals hierboven beschreven omdat de snelheidsboost (zoals de Lorents transformatie) tussen de bron en de waarnemer niet het gevolg is van het klassieke momentum en energieoverdracht maar wel het gevolg is van een verhoging in de golflengte van fotonen en roodverschuiving wanneer de ruimte waardoor ze reizen uitzet. Dit effect wordt omschreven als het huidige kosmologische model als een waarneembare manifestatie van de tijdsafhankelijke kosmische schaalfactor (a) in de volgende formule:
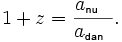
Dit soort roodverschuiving wordt de kosmologische roodverschuiving of de Hubble roodverschuiving genoemd. Indien het heelal inkromp in plaats van uitzetten zouden we verafgelegen sterrenstelsels een blauwverschuiving ondergaan door een hoeveelheid in verhouding met hun afstand in plaats van een roodverschuiving te ondergaan.
Deze sterrenstelsels gaan niet eenvoudig achteruit door middel van een fysieke snelheid in de richting weg van de waarnemer, in plaats daarvan zal de omliggende ruimte zich uitrekken welke geld voor de grootschalige isotropie van het effect aangeroepen door het kosmologische principe. Voor kosmologische roodverschuiving van z 0.1 zijn de effecten van de ruimtetijd uitzetting minimaal en de waargenomen roodverschuiving die gedomineerd wordt door de eigenaardige bewegingen van de sterrenstelsels relatief aan elkaar die de additionele Doppler roodverschuiving en blauwverschuiving veroorzaakt. Het verschil tussen de fysieke snelheid en de uitzetting van de ruimte is goed weergegeven door de uitzettende rubbervel heelal, een algemene kosmologische analogie die gebruikt wordt om de uitzetting van de ruimte te omschrijven. Indien twee objecten voorgesteld worden door kogellagers en ruimtetijd door een uitrekkend vel rubber, wordt het Doppler effect veroorzaakt door de ballen langsheen over het vel te bewegen zodat ze een beweging ondergaan. De kosmologische roodverschuiving gebeurt wanneer de kogellagers vast zitten op het vel en het vel uitgerekt wordt. (met dit model zijn er dimensionale problemen aangezien de kogellagers in het vel moeten zitten en de kosmologische roodverschuiving hogere snelheiden produceert dan Doppler als de afstand tussen de twee objecten ver genoeg is)
Ondanks het onderscheid tussen roodverschuiving veroorzaakt door de snelheid van objecten en de roodverschuiving verbonden met de uitzetting van het heelal refereren astronomen in de context soms "recessiesnelheid" van de roodverschuiving van verafgelegen sterrenstelsels van de uitzetting van het heelal, alhoewel het enkel een duidelijke recessie is. Als gevolg wordt in de literatuur soms de uitdrukking "Doppler roodverschuiving" gebruikt in plaats van "kosmologische roodverschuiving" om de beweging van sterrenstelsels te omschrijven die gedomineerd worden door de uitzetting van de ruimtetijd, ondanks het feit dat wanneer we het uitrekenen een "kosmologische recessiesnelheid" niet gelijk is aan de snelheid in de relativistische Dopplervergelijking. Doppler roodverschuiving is gebonden aan de speciale relativiteit, v > c dus en is onmogelijk terwijl in contrast v > c wel mogelijk is voor kosmologische roodverschuiving omdat de ruimte die tussen de objecten zit sneller kan uitzetten dan de snelheid van het licht. Het gezichtspunt dat "verafgelegen sterrenstelsels achteruitgaan" en het gezichtspunt dat "de ruimte tussen sterrenstelsels uitzet" zijn gerelateerd door veranderlijke coördinaatsystemen. Om dit precies uit te drukken is het vereist dat met werkt met de Friedman-Robertson-Walker meetkunde.
Gravitationele roodverschuiving
In de algemene relativiteitstheorie is er een tijdsdilatatie binnen een gravitationeel gat. Dit is gekend als de gravitationele roodverschuiving of Einstein verschuiving. De theoretische afleiding van dit effect volgt uit de Scgwarzschild oplossing van de Einstein vergelijkingen welke de onderstaande formule inhoud voor roodverschuiving, verbonden met een foton die reist in het gravitationele veld van een ongeladen, niet draaiende, sferisch symmetrische massa:
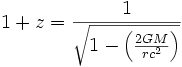
Waar:
- G staat voor de gravitationele constante
- M staat voor de massa van het object die het gravitationeel veld maakt
- r staat voor de radiale coördinaat van de waarnemer (welke analoog is aan de klassieke afstand van het centrum van het object maar eigenlijk een Schwarzschild coördinaat is
- c staat voor de lichtsnelheid
Deze gravitationele roodverschuiving resultaten kunnen afgeleid worden uit de speciale relativiteitstheorie en het gelijkwaardigheidsprincipe, de volledige algemene relativiteitstheorie is niet vereist.
Het effect is zeer klein maar wel meetbaar op Aarde door gebruik te maken van het Mossbauer effect en werd voor het eerst waargenomen in het Pound-Rebka experiment. Hoewel het aanzienlijk dicht bij een zwart gat ligt en het object de waarnemingshorizon bereikt dan wordt de roodverschuiving oneindig. Het is ook de dominante oorzaak van grote hoekschaal temperatuurschommelingen in de kosmische achtergrondstraling.







